

My degrees were awarded in 1985, 1987, and 1996 and I live in Lake Woebegone. Interesting too is that I have seen a graph of USCF ratings that has two "bumps", my presumption is that USCF ratings include two distinctly different populations, serious tournament playing adults, and a mix of scholastics.

From Table VIII, the p-value for n 9 with T 3.5 for a two-tailed test lies between 0.020 and 0.027, about 0.024.
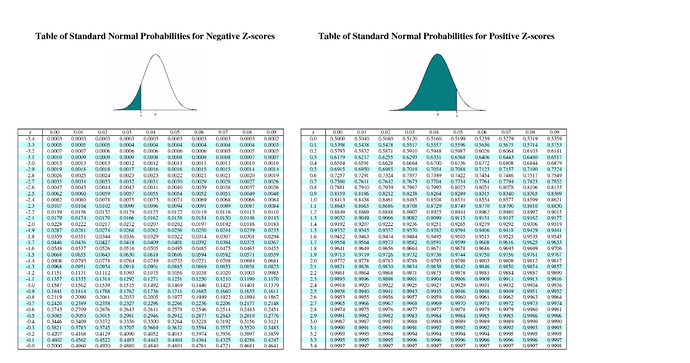
In either case the reality of the data is quite likely to stray from the "ideal" (model). Now, the standard normal score of the observed proportion is given by. But I don't have any more info than the graph to go on. It would be interesting to dig deeper to find out why. When graphed, the puzzle rating distribution looks close to a Poison too, but it is bumpy. In this case we know the lower bound of a chess rating is some fixed positive number (Someone mentioned 100) and we also know that the ratings are generated by a semi-random repetitive "process" (game outcomes), which is just the type of stuff the Poison is good for. Knowing how the data came to be is also a factor in choosing the right model. The first thing one should do with data is graph it, and then scrub it if necessary, and then choose a model. But to be clear, the rating distribution is closer to a Poison than a Normal. I'm sure pure math and stat people would be horrified at this interpretation, but I am an engineer, and the idea "works" for me. To me, and maybe just me, the Poison describes what happens to a normal distribution when you peg the left side to a lower bound (Zero?). If you need the left-tail probabilities, you’ll need to make a small additional calculation. The table provides the right-tail probabilities. The poison starts at zero and goes to positive infinity. Use the table below to find the chi-square critical value for your chi-square test or confidence interval or download the chi-square distribution table (PDF). The Normal distribution goes from negative to positive infinity. Using the mean of the poison you can calculate your percentile. The distribution in NOT a normal distribution.


 0 kommentar(er)
0 kommentar(er)
